EE982
-ELETROMAGNETISMO AVANÇADO
AULA 7 2013.01 PPGEE-UFPE
EXPANSÃO EM FUNÇÕES ORTOGONAIS
Funções ortogonais:
· Utilizadas de forma a simplificar a solução de problemas físicos (ex.: PVF em eletrostática, Eq. da onda, Eq. da difusão, Eq. de Schroedinger, etc.)
· Surgem naturalmente como soluções da equação diferencial que governa o problema físico.
· Tipo de função depende das coordenadas envolvidas
· Obedecem a relações simples de completeza e ortogonalidade
· Podem ser utilizadas como base de decomposição de uma função arbitrária.
7.1 Analogia com vetores
Considera base de vetores ortonormais
![]() no espaço
3-dimensional.
no espaço
3-dimensional.
Produto escalar: ![]()
Decomposição de um vetor: 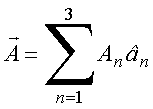 , com
, com
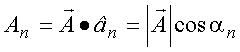
Copyrigth
1999-2013 by Eduardo Fontana
representa a projeção do vetor ![]() em
em ![]() e
e ![]() representa o ângulo entre esses vetores. Esse conceito
pode ser generalizado para funções, fazendo-se a definição
apropriada de produto escalar.
representa o ângulo entre esses vetores. Esse conceito
pode ser generalizado para funções, fazendo-se a definição
apropriada de produto escalar.
7.2 Produto escalar no espaço de funções
Sejam as funções complexas f
e g da variável real ![]() . Define-se o produto escalar por
. Define-se o produto escalar por
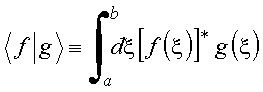
Note-se dessa definição que:
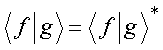
Ortogonalidade: as funções f e g são ortogonais se
![]()
7.3 Base de funções ortogonais
Seja ![]() , n=1, 2, 3, .... um conjunto de funções
ortogonais. Então
, n=1, 2, 3, .... um conjunto de funções
ortogonais. Então ![]() onde
onde ![]() é uma
constante que depende do parâmetro n. Podem-se definir
funções normalizadas na forma
é uma
constante que depende do parâmetro n. Podem-se definir
funções normalizadas na forma
Copyrigth
1999-2013 by Eduardo Fontana
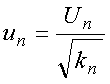
e essas funções satisfazem portanto a relação de ortogonalidade
![]()
As funções ![]() assim definidas formam um conjunto ortonormal de
funções no espaço
assim definidas formam um conjunto ortonormal de
funções no espaço ![]() .
.
Em analogia com a decomposição de um vetor em uma base ortonormal, o mesmo pode ser feito para o caso de funções, fazendo-se uso as relações de ortogonalidade. Ou seja, em princípio, é possível fazer a decomposição
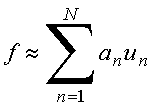
para algum valor grande de N. Os coeficientes podem ser determinados pela minimização do erro,
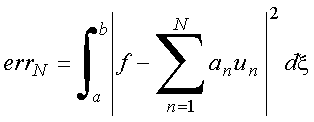
Pode-se mostrar que o mínimo da
função![]() , obtido de
, obtido de
Copyrigth
1999-2013 by Eduardo Fontana
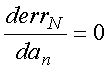
ocorre para
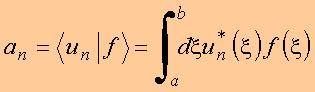
que é o mesmo resultado obtido para a decomposição de um vetor em uma base ortonormal.
A aproximação de f como
expansão em funções ortonormais torna-se cada vez melhor para
![]() . Nesse
regime diz-se que:
. Nesse
regime diz-se que:
a expansão converge para f na média.
7.4 Completeza
As condições para que as funções de base formem um conjunto completo são obtidas diretamente de
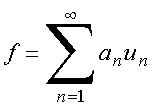
Utilizando ![]() , vem
, vem
Copyrigth
1999-2013 by Eduardo Fontana
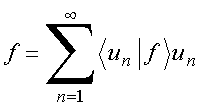
ou equivalentemente
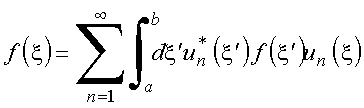
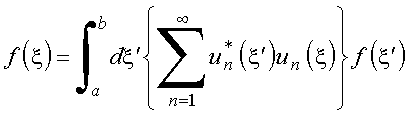
A última relação é para ser comparada com uma propriedade unívoca da função delta de Dirac.
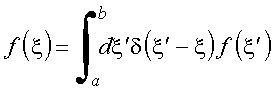
A unicidade da função ![]() permite concluir que
permite concluir que
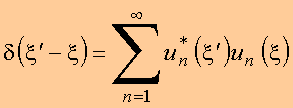
alternativamente
Copyrigth
1999-2013 by Eduardo Fontana
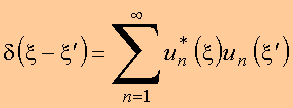
Todo conjunto completo de funções ortogonais, satisfaz as relações de completeza acima.
7.5 Exemplo: Série de Fourier de senos e cossenos
Consideremos o conjunto de funções
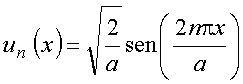
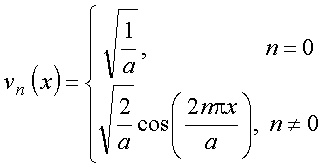
![]()
Propriedades:
![]()
![]()
![]()
Copyrigth
1999-2013 by Eduardo Fontana
Então:
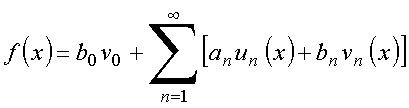
com
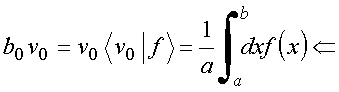 valor
médio de f
valor
médio de f
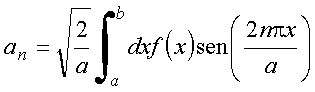
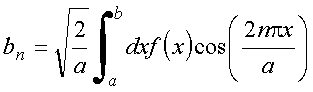
7.6 Exemplo: Série de Fourier de exponenciais complexas
Consideremos o conjunto de funções
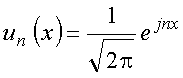
![]() e
e ![]()
Propriedades:
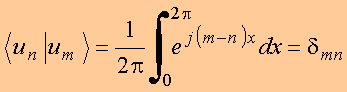
Copyrigth
1999-2013 by Eduardo Fontana
Completeza
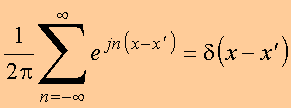
7.7 Conjunto contínuo de funções
Se o intervalo de definição das funções se tornar ilimitado, o conjunto discreto de funções se torna um contínuo de funções. As somas nesse caso se transformam em integrais, conforme no exemplo a seguir.
7.8 Integral de Fourier
Considera o conjunto de funções ortogonais
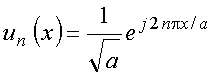
definidas com ![]() e
e ![]() . Tem-se
. Tem-se
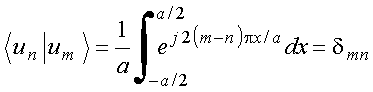
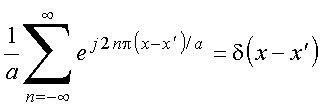
Copyrigth
1999-2013 by Eduardo Fontana
Fazendo ![]() define-se:
define-se:
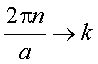
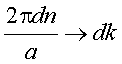 , onde dn=1
é o incremento na variável discreta n. Assim,
, onde dn=1
é o incremento na variável discreta n. Assim,
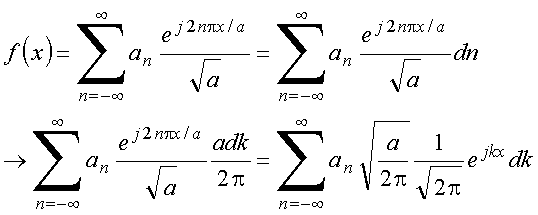
Fazendo
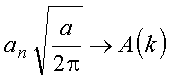
e notando que a soma é na realidade a definição de integral, obtém-se
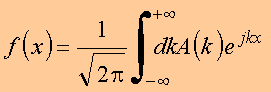
Copyrigth
1999-2013 by Eduardo Fontana
Note-se que
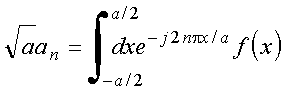
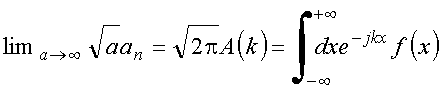
logo
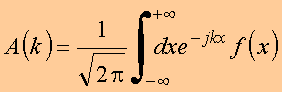
Completeza:
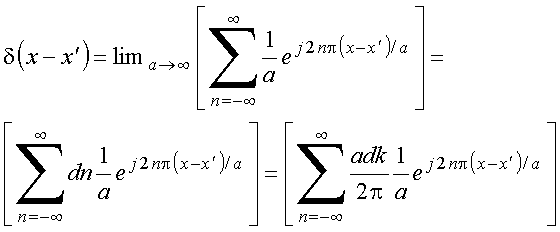
Copyrigth
1999-2013 by Eduardo Fontana
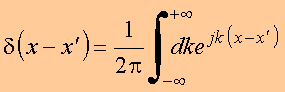
Note que isso pode ser observado como o processo limite
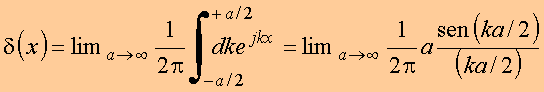
O processo está ilustrado no vídeo
abaixo
7.9 Expansão de funções de duas variáveis
Para o caso de funções de duas
variáveis definidas por ![]() ,
, ![]() e, por
exemplo, os conjuntos discretos de funções ortonormais u e
v satisfazendo às relações de ortogonalidade
e, por
exemplo, os conjuntos discretos de funções ortonormais u e
v satisfazendo às relações de ortogonalidade
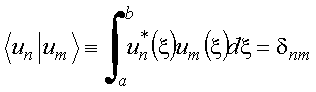
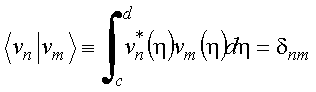
ou de forma compacta
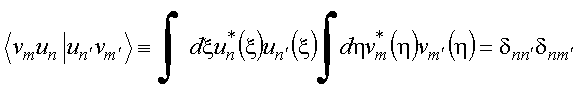 Copyrigth
1999-2013 by Eduardo Fontana
Copyrigth
1999-2013 by Eduardo Fontana
a expansão de uma função ![]() é da
forma
é da
forma
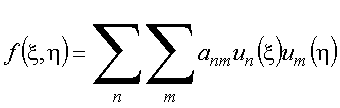
e os coeficientes são obtidos de
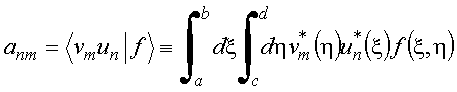
Copyrigth
1999-2013 by Eduardo Fontana