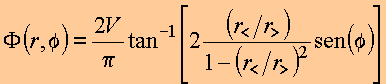EE982 -ELETROMAGNETISMO AVANÇADO
AULA 9 2013.01 PPGEE-UFPE
9.1
Separação de variáveis para problemas bi-dimensionais em
cilíndricas
Considera problemas bi-dimensionais governados pela eq. de Laplace em coordenadas cilíndricas
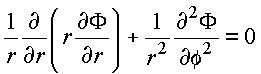
Assumindo
![]()
na equação diferencial, resulta em
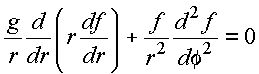
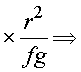
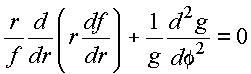
Copyrigth 1999-2013 by Eduardo Fontana
Utilizando o mesmo argumento da aula anterior, ambos os termos devem ser constantes para que o primeiro membro seja nulo. Seja a escolha

tem-se
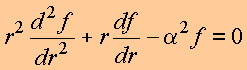

Caso 1: ![]()
Nesse caso, solução geral é da forma
![]()
Caso 2: ![]()
A solução geral da segunda equação diferencial é da forma
![]()
Para a primeira equação diferencial, pode-se assumir uma série de potências na variável r. Como mostrado a seguir, basta um termo da série para satisfazer a equação diferencial.
Copyrigth 1999-2013 by Eduardo Fontana
Assumindo portanto
![]()
na equação diferencial, tem-se
![]()
![]()
Portanto,
![]()
resultando em
![]()
Como antes, para uma dada classe de PVF, será necessário
utilizar uma combinação de soluções. O parâmetro ![]() , após aplicação das condições de contorno irá assumir
um conjunto de valores, e a solução geral pode sempre ser
expressa na forma
, após aplicação das condições de contorno irá assumir
um conjunto de valores, e a solução geral pode sempre ser
expressa na forma
Copyrigth 1999-2013 by Eduardo Fontana
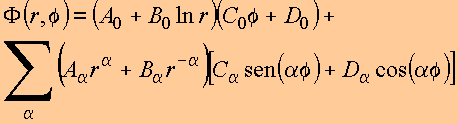
|
Observações: i. O termo logarítmico irá ocorrer se for colocada uma linha de carga na origem.
|
Alguns exemplos específicos são ilustrados a seguir.
Copyrigth 1999-2013 by Eduardo Fontana
Exemplo 9.1: Distribuição de potencial na vizinhança de uma superfície cilíndrica submetida a potencial arbitrário.
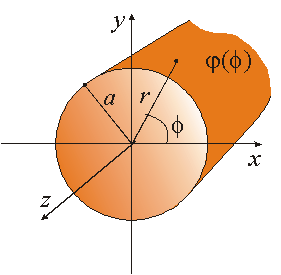
Para o PVF ilustrado na figura, pode-se mostrar que a solução no interior ou no exterior pode ser expressa na forma geral
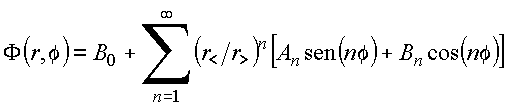
onde ![]() é o menor
(maior) entre r e a. Essa solução é finita na origem e no
infinito. Note-se que as funções
é o menor
(maior) entre r e a. Essa solução é finita na origem e no
infinito. Note-se que as funções ![]() (n
= 1, 2, 3, ...) e
(n
= 1, 2, 3, ...) e ![]() (n
= 0,1, 2, 3, ...), no espaço
(n
= 0,1, 2, 3, ...), no espaço ![]() satisfazem
às relações de ortogonalidade
satisfazem
às relações de ortogonalidade
![]()
![]()
Copyrigth 1999-2013 by Eduardo Fontana
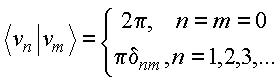
Com essas relações de ortogonalidade, a condição de contorno
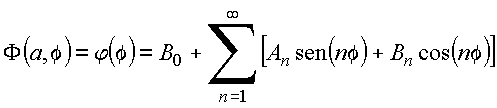
ou equivalentemente
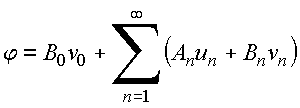
é satisfeita para
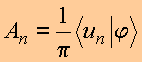
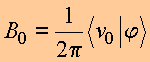

ou seja,

Copyrigth 1999-2013 by Eduardo Fontana

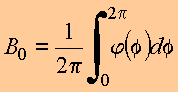
![]() valor médio da função
valor médio da função
Consideremos por exemplo a situação de eletrodos cilíndricos submetidos às condições de contorno da figura.

Tem-se
![]()
![]()
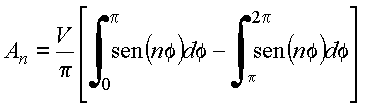
Copyrigth 1999-2013 by Eduardo Fontana
o que fornece

ou seja
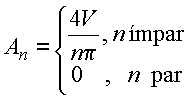
Logo, a solução no interior ou no exterior é dada por

Como mostrado na aula anterior é possível obter uma solução fechada para esse problema. Sejam as definições
![]()
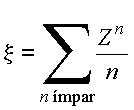
então
Copyrigth 1999-2013 by Eduardo Fontana
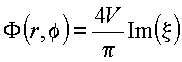
Utilizando
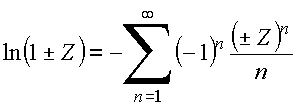
vem
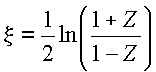
Definindo
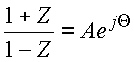
tem-se
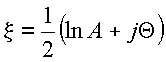
Portanto

Como mostrado na aula anterior
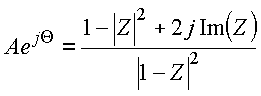
e portanto
Copyrigth 1999-2013 by Eduardo Fontana
|
|
A variação espacial da função potencial está simulada no
vídeo abaixo. Nesse vídeo, a diferença de potencial é variada
continuamente entre os eletrodos de um valor positivo para um
valor negativo. A distribuição de potencial se assemelha ao
perfil de uma membrana elástica esticada por dois objetos
semi-circulares acionados em sentidos opostos. Na realidade, a
distribuição de alturas de uma membrana nessas condições
satisfaz a equação de Laplace.
Copyrigth 1999-2013 by Eduardo Fontana
Exemplo 9.2: Seja agora o PVF mostrado na figura seguinte.

Para essa situação, a solução com periodicidade na
variável ![]() não pode ser utilizada, uma vez que é necessário a
utilização de funções de base na variável radial para sintetizar
a função
não pode ser utilizada, uma vez que é necessário a
utilização de funções de base na variável radial para sintetizar
a função ![]() mostrada
na figura.
mostrada
na figura.
Para obter um conjunto adequado de funções para o
presente problema, seja a constante de separação sendo
modificada de acordo com ![]() . Com essa substituição,
. Com essa substituição,
![]()
Para a função radial obtém
Copyrigth 1999-2013 by Eduardo Fontana
![]()
Essa forma não é muito conveniente, pois envolve grandezas complexas e a função potencial é uma função real. Para determinar-se uma forma real alternativa para f , seja a definição
![]()
ou equivalentemente
![]()
o que fornece
![]()
com
![]() .
.
Com essa definição duas combinações envolvendo as funções r±ja podem ser obtidas
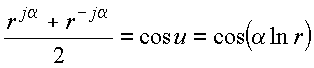
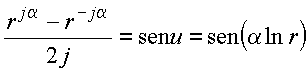
Copyrigth 1999-2013 by Eduardo Fontana
Assim, as funções ![]() e
e ![]() formam um
par de funções reais e independentes que permitem expressar a
função radial na forma
formam um
par de funções reais e independentes que permitem expressar a
função radial na forma
![]()
Uma forma equivalente é
![]()
que satisfaz a condição ![]()
Com essa
escolha para a constante a, uma
solução possível para a Eq. de Laplace é da forma
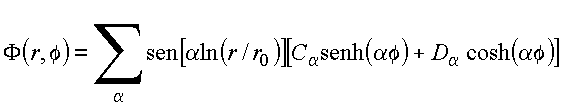
Com essa escolha, aplicando-se a
condição de fronteira no trecho nas superfícies ![]() e r=a reduz a função potencial para a
forma
e r=a reduz a função potencial para a
forma

Copyrigth 1999-2013 by Eduardo Fontana
A condição de fronteira em r=b é satisfeita pela escolha


Aplicando-se
a condição de fronteira na superfície ![]() resulta
resulta
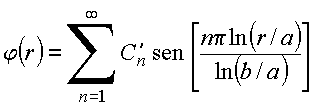
com

As funções
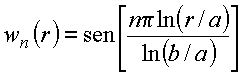
Copyrigth 1999-2013 by Eduardo Fontana
estão plotadas na figura seguinte e obedecem a relações de ortogonalidade. O produto escalar para essa classe de funções obedece à definição
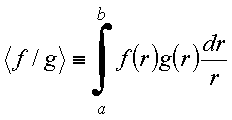

Copyrigth 1999-2013 by Eduardo Fontana
Com
essa definição do produto escalar, tem-se

Fazendo-se a mudança de variáveis
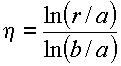
tem=se

ou equivalentemente
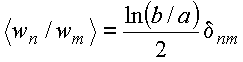
Com essa definição, obtém-se
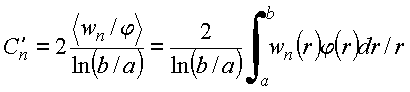 .
.
E portanto
Copyrigth 1999-2013 by Eduardo Fontana
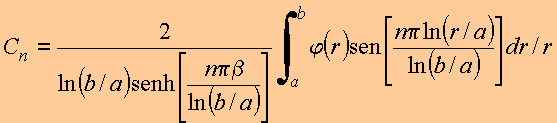
Copyrigth 1999-2013 by Eduardo Fontana