ELETROMAGNETISMO AVANÇADO
AULA 16 2013.1 PPGEE-UFPE
EXPANSÃO DA FUNÇÃO INVERSA EM COORDENADAS CILÍNDRICAS
Seja
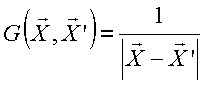
Dado
que:
em
cilíndricas:
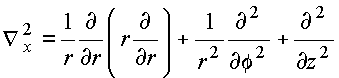
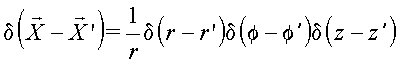
Copyrigth 1999-2013 by Eduardo
Fontana
Usa as
relações de completeza:
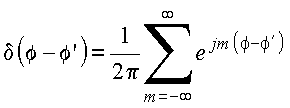
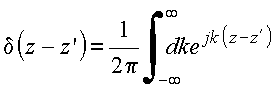
Expande G na
forma:
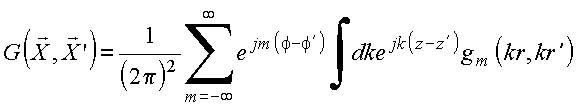
Note-se
que a função 
depende dos
parâmetros m e k.
Inserindo essas expansões na equação diferencial, e igualando ambos os membros termo a termo, vem
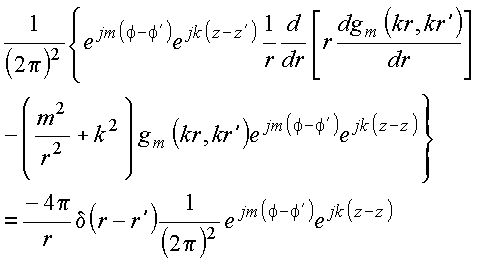
Copyrigth 1999-2013 by Eduardo
Fontana
ou equivalentemente
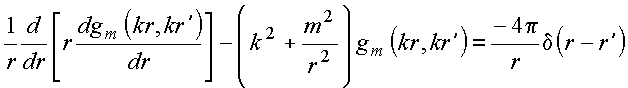
Como mostrado na aula anterior, para obter
:
Caso 1: 
A equação diferencial reduz-se para
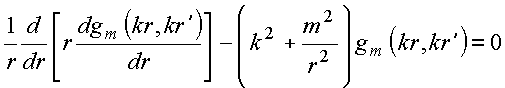
Note-se que a
função 
causa
descontinuidade
na derivada de 
, e conseqüentemente, funções distintas devem ser
utilizadas
para 
e 
. Essas
funções têm o
mesmo valor em 
, mas as derivadas são distintas. Note-se que essa equação tem a estrutura
da equação diferencial
que gera as funções modificadas de Bessel, e portanto, a
estrutura geral de
cada solução é do tipo,
Copyrigth 1999-2013 by Eduardo
Fontana
Alternativamente, essa combinação poderia ser escrita na forma
com 
sendo constantes independentes de 
. Expandindo essa última expressão
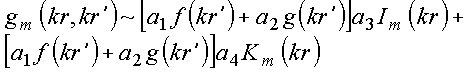
e as duas expressões são equiavalentes se
Ou seja, a solução pode ser escrita como o produto de duas funções de argumentos distintos,
com a dependência em r sendo uma combinação de funções modificadas de Bessel. Seja portanto, a forma geral da solução
:
:
Copyrigth 1999-2013 by Eduardo
Fontana
com 
sendo
combinações de
funções modificadas de Bessel. Pela propriedade de simetria da
função de Green,
tem-se
que pode ser verificado se
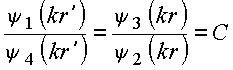
Sem perda de generalidade, C =1 (o valor da constante C pode ser inserido em uma das funções), logo
Ou seja, ambas
as funções que
compõe o produto 
são combinações de funções modificadas de Bessel. Assim
:
:
Copyrigth 1999-2013 by Eduardo
Fontana
ou equivalentemente
De volta a equação diferencial
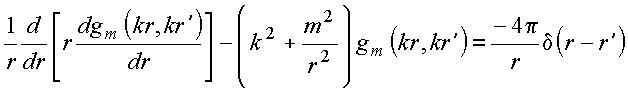
integrando ambos
os membros em
torno de 
, vem
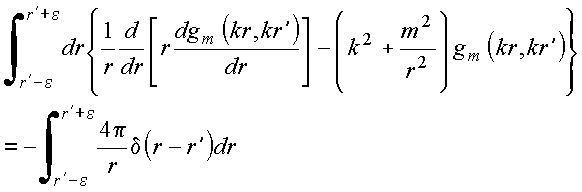
Donde:
Copyrigth 1999-2013 by Eduardo
Fontana
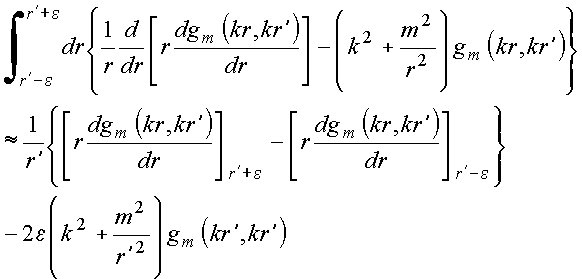
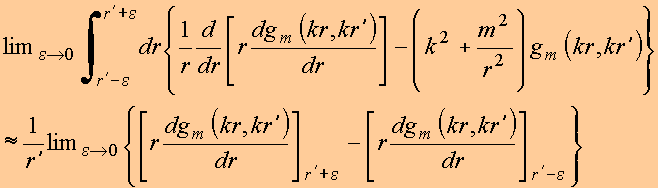
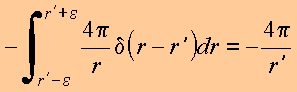
Copyrigth 1999-2013 by Eduardo
Fontana
Igualando essas duas últimas relações, vem
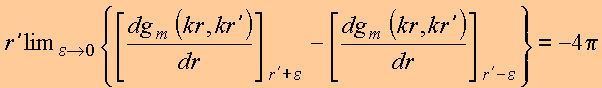
Calculando as derivadas, tem-se
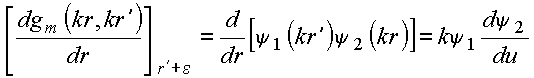
com
(em 
)
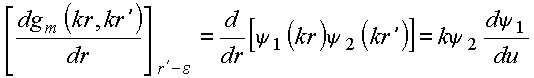
Logo
donde
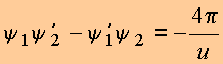
Copyrigth 1999-2013 by Eduardo
Fontana
Define-se o Wroskiano associado à equação diferencial pela relação
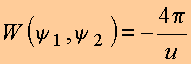
Uma outra forma de mostrar que o Wroskiano é dado por essa expressão pode ser obtida parametrizando-se a equação diferencial homogênea em função da variável u. Tem-se
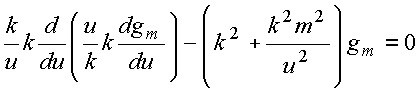
ou equivalentemente
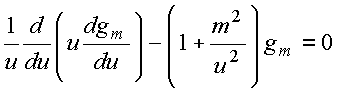
ou ainda
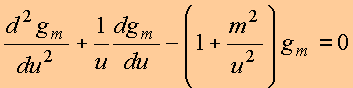
Copyrigth 1999-2013 by Eduardo
Fontana
Seja
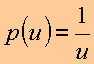
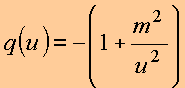
Então a equação diferencial é do tipo
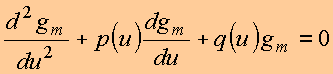
Sendo 
as
funções que
compõem o produto. Como
ambas são
combinações de funções modificadas de Bessel tem-se
ou equivalentemente
Note-se que o Wroskiano
tem a propriedade
Copyrigth 1999-2013 by Eduardo
Fontana
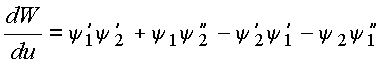
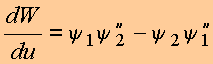
Com base na eq. diferencial, essa última relação pode ser posta na forma
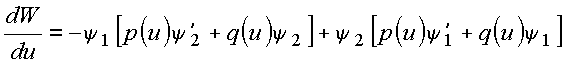
donde
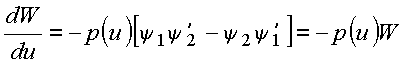
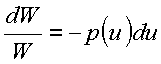
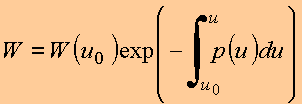
Copyrigth 1999-2013 by Eduardo
Fontana
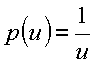
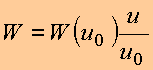
ou seja
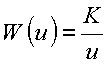
Que é a mesma forma obtida anteriormente com K = 1.
Considerações
físicas
A solução radial é finita na origem e no infinito o que reduz a forma da solução para
O Wroskiano é
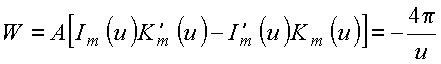
Copyrigth 1999-2013 by Eduardo
Fontana
Para determinar a constante usa comportamento assintótico das funções modificadas, i.e.,
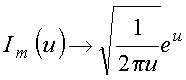
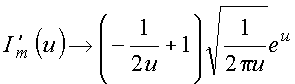
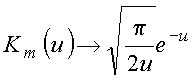
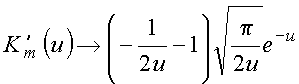
o que fornece
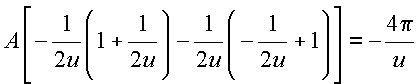
Donde
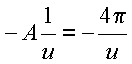
o que fornece
Copyrigth 1999-2013 by Eduardo
Fontana
e a expansão da função inversa em cilíndricas pode ser posta na forma
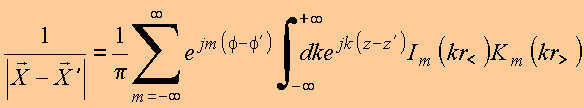
Copyrigth 1999-2013 by Eduardo
Fontana