ELETROMAGNETISMO AVANÇADO
AULA 18 2013.1 PPGEE-UFPE
18.1. PROBLEMAS
DE VALORES
DE FRONTEIRA ENVOLVENDO MEIOS MATERIAIS DISTINTOS
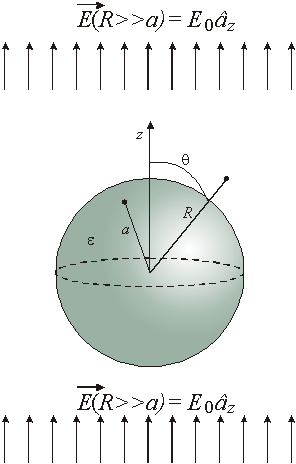
Exemplo 1: esfera dielétrica
em uma região de
campo uniforme
Considera
uma
esfera dielétrica de raio a e
permissividade ![]() , colocada em uma região de campo
uniforme:
, colocada em uma região de campo
uniforme:
·
Qual a distorção produzida nas linhas
de campo?
·
Qual é o campo no interior da esfera?
Copyrigth 1999-2013 by Eduardo
Fontana
Com
![]() , temos
de obter a
função potencial como solução
, temos
de obter a
função potencial como solução
da
equação
de Laplace, ![]() .
.
1.
Separa
o
espaço em duas regiões:
![]()
i.
Campo
uniforme para ![]()
![]()
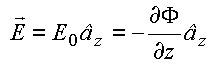
ou
seja,
![]()
ii.
Condições
de contorno
![]()
![]() ,
,
ou
equivalentemente
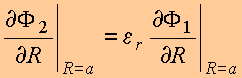
com
![]()
Copyrigth 1999-2013 by Eduardo
Fontana
iv.
Simetria
azimutal
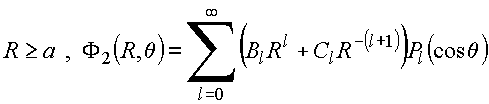
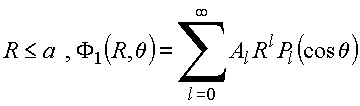 (finito
na
origem)
(finito
na
origem)
2.
Aplica
condições de contorno:
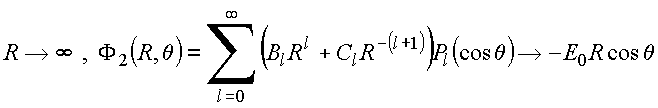
![]()
![]()
Em ![]()
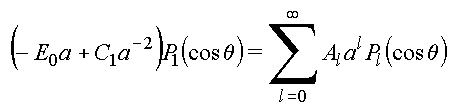
![]() (1)
(1)
Copyrigth 1999-2013 by Eduardo
Fontana
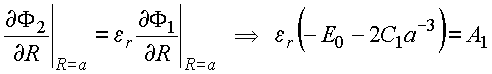 (2)
(2)
A
solução de (1) e (2) fornece
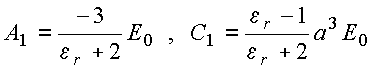
Em resumo:
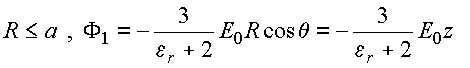
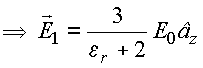 (campo
uniforme no
dielétrico)
(campo
uniforme no
dielétrico)
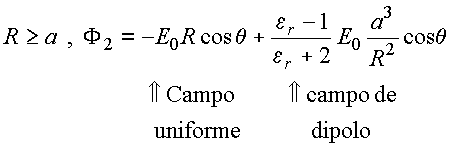
O
campo no exterior é a soma do campo uniforme mais o campo
induzido que
corresponde ao efeito de um dipólo localizado na origem, com momento de dipólo
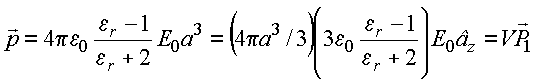
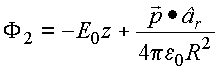
Copyrigth 1999-2013 by Eduardo
Fontana
O
campo no interior da esfera é enfraquecido devido às cargas de
polarização que
se localizam na superfície. Essas cargas geram um campo
interno em oposição ao
campo aplicado. A densidade superficial de cargas de
polarização pode ser
obtida da relação:
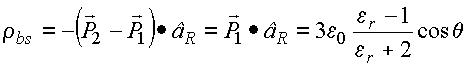
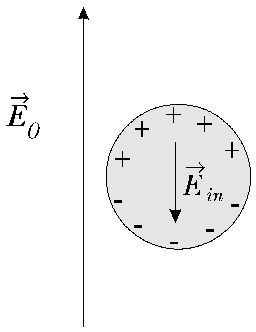
Copyrigth 1999-2013 by Eduardo
Fontana
18.2 MÉTODO DAS IMAGENS EM
MEIOS MATERIAIS
DISTINTOS
Considera a determinação da função potencial quando a distribuição de carga está localizada em um meio dielétrico conforme ilustrado na figura
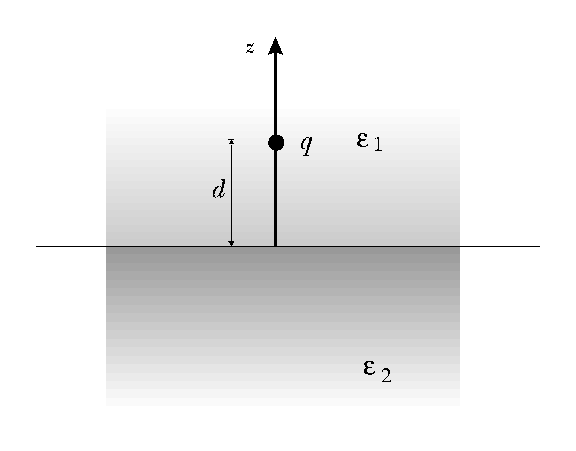
·
Como obter o potencial nas duas
regiões?
·
Pode-se aplicar o método das imagens
nesse caso?
Para obter a solução do
problema, notemos que:
![]()
Devido
a
simetria azimutal, usa o sistema de coordenadas cilíndricas. A
densidade de
carga associada à carga puntiforme localizada em ![]() é
é
Copyrigth 1999-2013 by Eduardo
Fontana
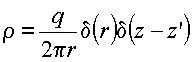
O
potencial em cada região pode ser expresso como integral de
Fourier-Bessel:
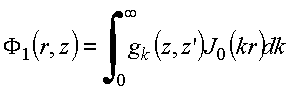
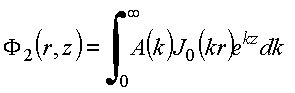
·
No meio 1, a
função ![]() será
determinada
resolvendo a equação de Poisson.
será
determinada
resolvendo a equação de Poisson.
·
No meio 2, a dependência em z da função potencial é da forma ![]() pois
o
potencial é solução da eq. de Laplace, e deve ser finito para
pois
o
potencial é solução da eq. de Laplace, e deve ser finito para
![]() .
.
De
volta
à equação para ![]() ,
utilizando a
relação
,
utilizando a
relação
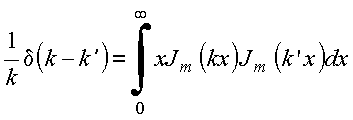
com
m=0,
![]() , obtém
, obtém
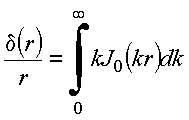
Copyrigth 1999-2013 by Eduardo
Fontana
Insere na equação de
Poisson, obtém
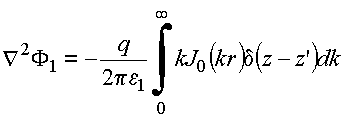
Usa laplaciano expresso em cilíndricas, obtém:
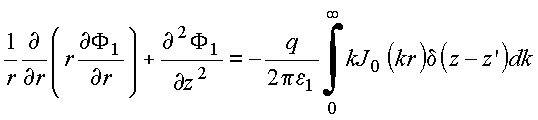
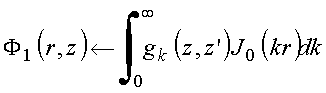
![]()
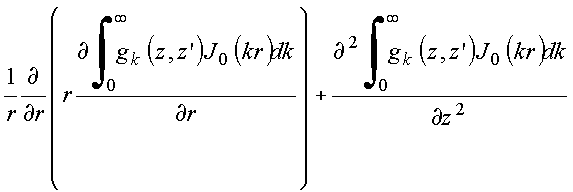
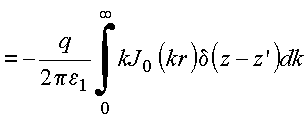
Copyrigth 1999-2013 by Eduardo
Fontana
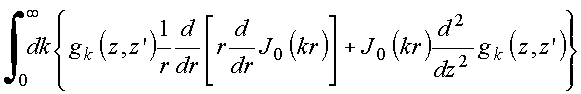
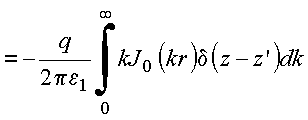
A
função de Bessel de ordem zero, satisfaz à equação,
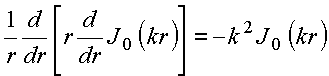
Logo,
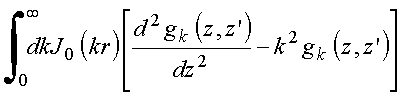
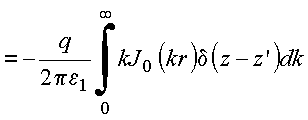
Para que as duas expansões sejam iguais, é necessário que os coeficientes da função de bessel em ambos os membros sejam iguais, resultando:
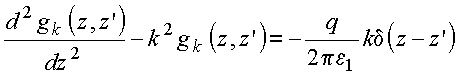
Copyrigth 1999-2013 by Eduardo
Fontana
Para resolver a
equação diferencial
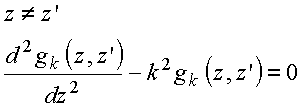
(z´=
d corresponde à posição da carga discreta)
Soluções:
![]()
![]()
simetria:
![]()
Portanto
a
solução é da forma:
![]()
Descontinuidade
na
derivada é obtida integrando em torno do ponto z = z' , resultando em:
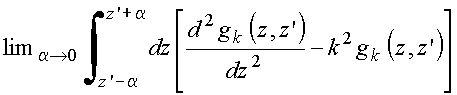
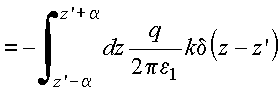
Copyrigth 1999-2013 by Eduardo
Fontana
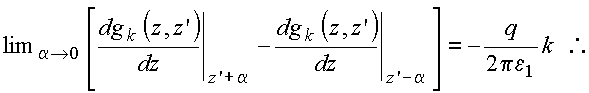
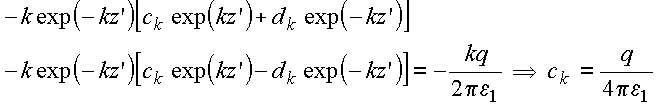
a
função ![]() é
da
forma:
é
da
forma:
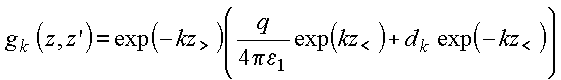
para
determinar
o coeficiente ![]() ,
bem como o potencial na região
,
bem como o potencial na região ![]() ,
aplica as
condições de contorno em
,
aplica as
condições de contorno em ![]() :
:
![]() :
:
![]()
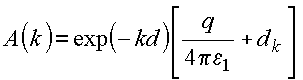 (1)
(1)
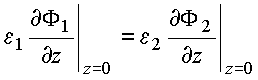
Copyrigth 1999-2013 by Eduardo
Fontana
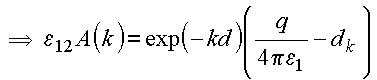 (2)
(2)
![]()
Resolvendo
(1)
e (2), resulta:
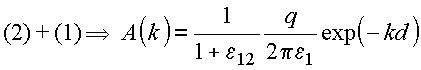
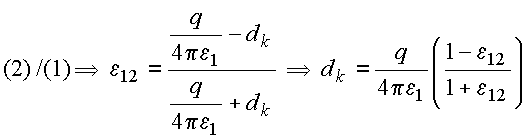
Soluções:
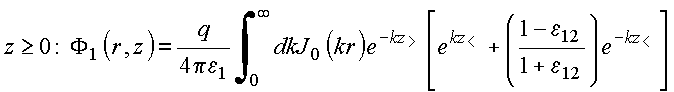
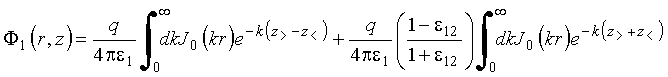
usa
a
expansão:
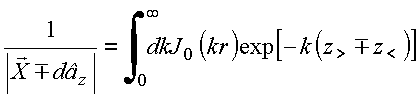
Copyrigth 1999-2013 by Eduardo
Fontana
obtém:
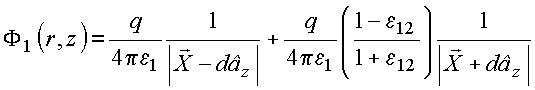
Na
região
![]() ,
obtém:
,
obtém:
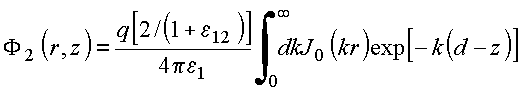
Com base na expansão da função inversa, resulta em
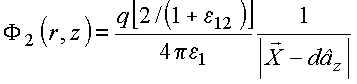
INTERPRETAÇÃO:
Define
as
grandezas:
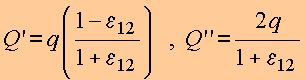
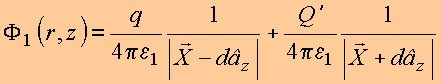
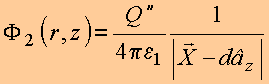
Copyrigth 1999-2013 by Eduardo
Fontana
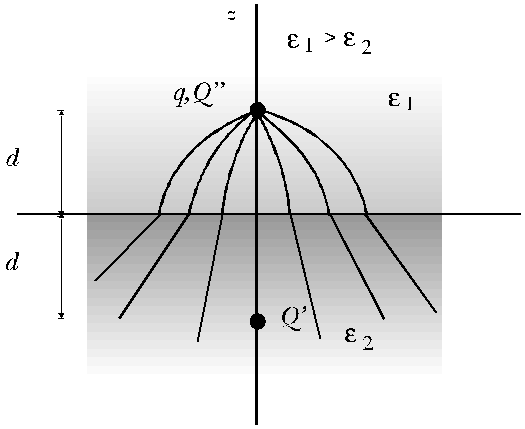
·
Na região ![]() , o problema é
equivalente à soma dos
potenciais da carga original q e
carga imagem Q' localizada
em
, o problema é
equivalente à soma dos
potenciais da carga original q e
carga imagem Q' localizada
em ![]() , com a região
, com a região ![]() substituida
pelo
meio 1
substituida
pelo
meio 1
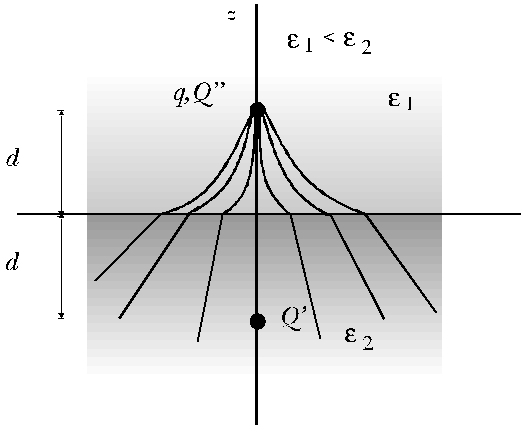
·
Na região ![]() , o problema é equivalente ao
potencial gerado por uma carga equivalente Q'', localizada em z=d,
também com a região
, o problema é equivalente ao
potencial gerado por uma carga equivalente Q'', localizada em z=d,
também com a região ![]() substituida
pelo
meio 1
substituida
pelo
meio 1
· Se ![]()
· Se ![]()
Copyrigth 1999-2013 by Eduardo
Fontana
Copyrigth 1999-2013 by Eduardo
Fontana
18.3 ENERGIA EM MEIOS
MATERIAIS
Considera
um
meio material mapeado pelas grandezas, ![]() e
e
![]() . Um incremento
diferencial
. Um incremento
diferencial ![]() na
região
em que o potencial é
na
região
em que o potencial é ![]() , produz um
incremento de energia:
, produz um
incremento de energia:
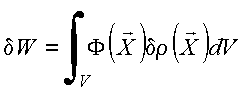
A energia no
estado final do
sistema é obtida variando a densidade de carga desde um valor
nulo até um valor
final ![]() , ou seja
, ou seja
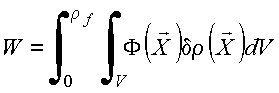
Alternativamente
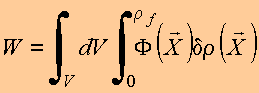
Essa é a expressão mais geral da energia de uma distribuição de cargas, que independe do tipo de meio material.
Se o
meio em questão é
linear, pode-se definir uma variável adimensional u,
![]() tal que
tal que
![]()
Copyrigth 1999-2013 by Eduardo
Fontana
![]()
então
![]()
Dessas relações tem-se
![]()
logo
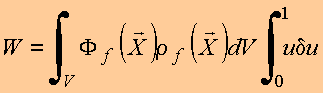
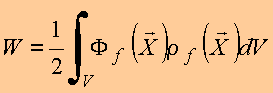
Para obter a expressão geral no ponto de vista do campo, considera
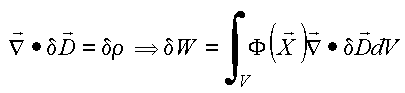
![]()
Copyrigth 1999-2013 by Eduardo
Fontana
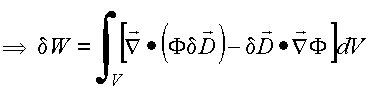
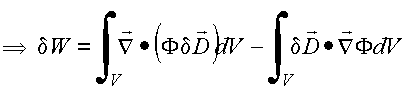
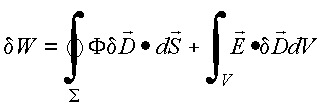
Escolhe
a
superfície ![]() envolvendo
todo
o espaço
envolvendo
todo
o espaço
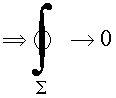 ,
,
logo
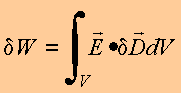
Para
computar
a energia contida na região de campo, calculamos a energia
total W , começando
com campo nulo, resultando
em
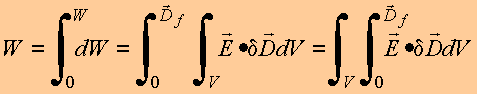
Essa é a expressão geral para a energia
Copyrigth 1999-2013 by Eduardo
Fontana
·
Para meio linear anisotrópico (meio
isotrópico é um
caso particular)
![]()
![]()
Para meios sem perdas,
![]()
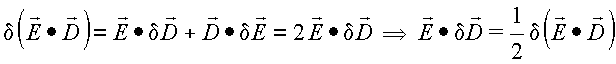
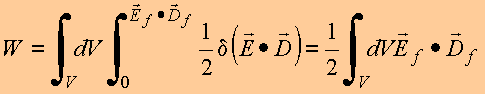
Sumário:
·
Meio não-linear :
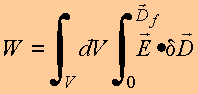
ou
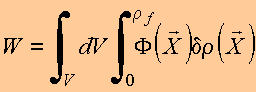
Copyrigth 1999-2013 by Eduardo
Fontana
·
Meio linear:
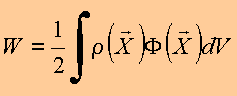
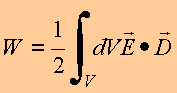
Copyrigth 1999-2013 by Eduardo
Fontana