ELETROMAGNETISMO AVANÇADO
AULA 25 2013.1 PPGEE-UFPE
25.1 Corrente de Deslocamento, equações de Maxwell, condições de contorno
Obtido até a lei de
Faraday
![]() (1)
(1)
 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
A Eq.(4) viola o princípio
da conservação da
carga
A corrente
para fora da região
volumétrica
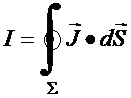
Copyrigth 1999-2013 by Eduardo Fontana
deve
corresponder à taxa de
diminuição na carga no volume, ie.,

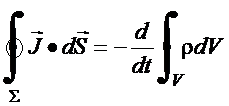
ou para uma geometria fixa
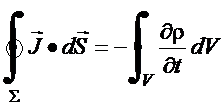
A forma diferencial é
obtida do teorema de
Gauss o que fornece

Por outro lado
a lei de Ampère
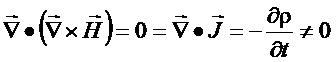
viola o princípio da
conervação da carga
Note que da Eq.(1)
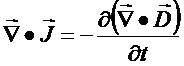
Copyrigth 1999-2013 by Eduardo Fontana

Maxwell denominou o
parâmetro  pelo
termo “densidade de corrente de deslocamento” e assumiu
que a correção
necessária seria portanto a adição desse termo no segundo
membro da Eq.(4),
i.e.
pelo
termo “densidade de corrente de deslocamento” e assumiu
que a correção
necessária seria portanto a adição desse termo no segundo
membro da Eq.(4),
i.e.
![]()
 (satisfaz a
equação da continuidade)
(satisfaz a
equação da continuidade)
A corrente de deslocamento
resolve, por
exemplo, o paradigma ilustrado na figura.

Copyrigth 1999-2013 by Eduardo Fontana
Na ausência dessa
componente

No entanto, ![]() sobre
sobre
![]() e sobre
e sobre
![]()
![]() , e
portanto a expressão
acima é inconsistente
, e
portanto a expressão
acima é inconsistente
Com a inclusão da corrente
de deslocamento
tem-se


Com a inclusão da corrente
de deslocamento as
equações de Maxwell se tornam:
![]() (1)
(1)
 (2)
(2)
![]() (3)
(3)
 (4´)
(4´)
Copyrigth 1999-2013 by Eduardo Fontana
A lei de Faraday
estabelece que um campo
magnético variante no tempo gera um campo elétrico. A Eq.(4’)
representa o efeito recíproco,
i.e., um campo elétrico variante no tempo induz um campo
campo magnético.
As relações constitutivas
em meios materiais
envolvem os vetores polarização e magnetização.
Em meios condutores há também uma conexão entre os
vetores campo
elétrico e densidade de corrente, ou seja,
![]() (A)
(A)
![]() (B)
(B)
![]() (C)
(C)
É importante observar que
mesmo em meios
lineares, para campos variantes no tempo em geral, não há
um fator de escala
que torne os campos múltiplos um do outro, no caso
elétrico ou no caso
magnético. Em geral, o fenômeno de dispersão em meios
lineares, faz com que perturbações
do vetor campo elétrico e do vetor densidade de fluxo
elétrico não tenham a
mesma fase. O mesmo ocorre no caso magnético.
No entanto, os harmônicos das grandezas de campo,
em meios lineares,
diferem por um fator de escala (permissividade elétrica ou
permeabilidade
magnética, ou condutividade elétrica) na freqüência do
harmônico
correspondente.
As condições de contorno
para as grandezas de
campo, são obtidas de uma das formas integrais das
equações de Maxwell, i.e.,
Copyrigth 1999-2013 by Eduardo Fontana
 (5)
(5)
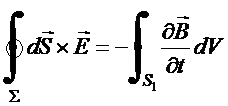 (6)
(6)
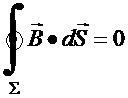 (7)
(7)
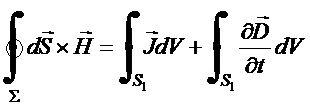 (8)
(8)

Utilizando a superfície
fechada mostrada na
figura, no limite ![]() , obtém
, obtém
Copyrigth 1999-2013 by Eduardo Fontana
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
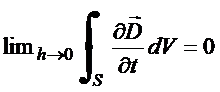

No regime transitório do
estabelecimento de
campos elétricos estáticos ou no regime permanente desses
campos, cargas de
superfície podem existir na superfície de um condutor
imperfeito. Da mesma
forma, no regime de corrente estacionária cargas de
superfície surgem na
superfície de contato entre condutores distintos.
Para campos variantes no
tempo, as densidades
superficiais de carga ![]() e de
corrente
e de
corrente ![]() são
idealizações em superfícies de condutores perfeitos. Para meios reais
de condutividade finita, os
campos podem penetrar no material até uma extensão que
depende da freqüência
das oscilações do campo, e de fato, os termos idealizados
de superfície são
nulos, ou seja:
são
idealizações em superfícies de condutores perfeitos. Para meios reais
de condutividade finita, os
campos podem penetrar no material até uma extensão que
depende da freqüência
das oscilações do campo, e de fato, os termos idealizados
de superfície são
nulos, ou seja:
Para condutores perfeitos:
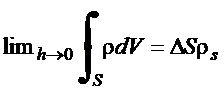
Copyrigth 1999-2013 by Eduardo Fontana
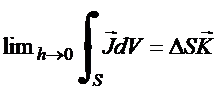
Superfícies de condutores
reais (caso dinâmico):
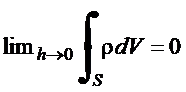
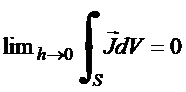
e as condições de contorno
se reduzem a (caso
dinâmico):
![]() (9´)
(9´)
![]() (10)
(10)
![]() (11)
(11)
![]() (12´)
(12´)
25.2 Potencial vetor e escalar
A introdução de funções
potenciais permite
obter um número reduzido de equações para a solução de
problemas
eletromagnéticos.
No caso eletrostático
![]() ,
, ![]()
Copyrigth 1999-2013 by Eduardo Fontana
No caso magnetostático
![]() ,
, ![]()
Em ambos os casos basta
determinar os
respectivos potenciais das equações não-homogêneas e as
grandezas de campo
ficam determinadas.
Para campos variantes no
tempo, as equações de
Maxwell são reescritas na forma
Equações homogêneas
(ausência de fontes no
segundo membro):
 (1)
(1)
![]() (3)
(3)
Equações não-homogêneas
(presença de fontes no
segundo membro):
![]() (2)
(2)
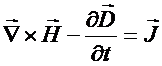 (4)
(4)
Definição dos potenticais:
Copyrigth 1999-2013 by Eduardo Fontana
De (3) pode definir o
potencial vetor magnético
![]() pela relação
pela relação
![]() (13)
(13)
Insere em (a) obtém
 (14)
(14)
Essa relação permite
definer o potencial
escalar de

ou equivalentemente
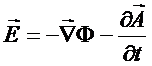 (15)
(15)
Em resumo, determinados ![]() , os
campos são
determinados de:
, os
campos são
determinados de:
![]() (13)
(13)
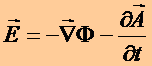 (15)
(15)
Copyrigth 1999-2013 by Eduardo Fontana
Equações diferenciais para os potenciais no vácuo
Rigorosamente, o vácuo é o
único meio em que há
uma relação linear entre campos. Com o emprego de (A) e
(B) nas equações
não-homogêneas, obtêm-se as equações diferenciais para os
potenciais. Considerando
a determinação dos campos no vácuo, i.e.,
![]() (D)
(D)
![]() (E)
(E)
Inserindo (D) em (2) com o
auxílio de (15)
obtém
 (16)
(16)
Inserindo (E) em (4) com o
auxílio de (13)
obtém

![]()
obtém
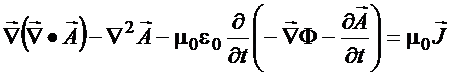
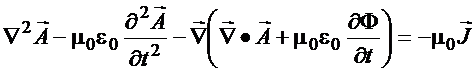
Copyrigth 1999-2013 by Eduardo Fontana
Definindo a velocidade da
luz por
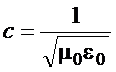 (17)
(17)
obtém
 (18)
(18)
Em resumo, as equações
diferenciais para os
potenciais são
 (16)
(16)
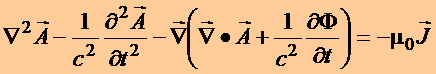 (18)
(18)
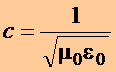 (17)
(17)
Observações:
·
Obtém-se apenas duas
equações para os
potenciais ( embora a equação para o potencial vetor
corresponda a três
equações)
·
Inconveniente é que as
equações são acopladas.
As equações podem ser
desacopladas no âmbito da
liberdade de escolha do divergente do potencial vetor, o
que define as
transformações de gauge.
Copyrigth 1999-2013 by Eduardo Fontana
25.3 Transformações de gauge, gauge de Coulomb e de Lorentz
Transformações das funções
potenciais podem ser
realizadas desde que preservem a unicidade das grandezas
de campo. Essas
transformações são denominadas de
“transformações de gauge”.
Originamente
![]() (13)
(13)
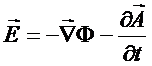 (15)
(15)
Define a transformação,
dentro da liberdade de
escolha do divergente do potencial vetor,
![]() (19)
(19)
Nesse novo
gauge,
![]()
ou seja o vetor B não é
alterado nessa
transformação
Que modificação é
produzida em E?

Para que o campo permaneça
inalterado é
necessário fazer
Copyrigth 1999-2013 by Eduardo Fontana

e portanto
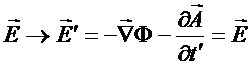
Em resumo, para manter os
campos invariante, os
potenciais podem ser transformados de acordo com a
transformação de gauge
![]() (20)
(20)
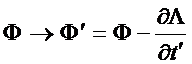 (21)
(21)
Gauge de Lorentz
Um tipo de transformação
de gauge coloca os
potenciais no gauge de Lorentz, i.e., se o divergente do
potencial vetor for escolhido
na condição de Lorentz
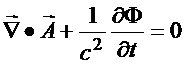 (22)
(22)
Nessa condição, as
equações diferenciais para
os potenciais se tornam
 (23)
(23)
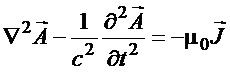 (24)
(24)
Copyrigth 1999-2013 by Eduardo Fontana
Essas são equações
desacopladas não-homogêneas
e ambas representam a equação da onda não-homogênea. Ou seja, a
condição de Lorentz é útil pois
resulta em um par de equações diferenciais desacopladas. É importante
notar que é sempre possível
realizar uma transformação de gauge tal que a condição de
Lorentz é
satisfeita. Para
isso, suponha que os
potenciais não satisfazem inicialmente à condição de
Lorentz. Ou
seja, para um dado par de funções potenciais,
tem-se
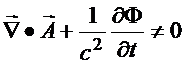
Fazendo a transformação de gauge
![]()
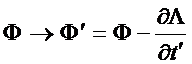
e impondo que os novos
potenciais satisfaçam à
condição

tem-se
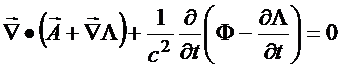
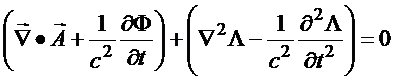
Copyrigth 1999-2013 by Eduardo Fontana
ou equivalentemente
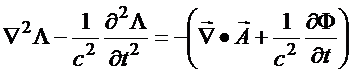 (25)
(25)
Assim, a função ![]() deve satisfazer à
essa equação da onda
não-homogênea.
deve satisfazer à
essa equação da onda
não-homogênea.
Por exemplo, o conjunto de
potenciais que
satisfazem à condição de Lorentz tem a função de
transformação de gauge,
satisfazendo à equação da onda homogênea
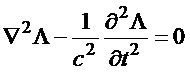
Gauge de Coulomb
O gauge de Coulomb é
obtido da condição
![]() (26)
(26)
Da equação diferencial
para o potencial escalar
obtém
 (27)
(27)
que é a equação de Poisson
Por exemplo, se há uma
distribuição de carga
localizada em uma região ilimitada, a solução da equação
de Poisson é a mesma
obtida anteriormente, i.e.,
Copyrigth 1999-2013 by Eduardo Fontana
 (28)
(28)
Nesse gauge ![]() é o potencial
coulombiano instantâneo em um
ponto de coordenadas
é o potencial
coulombiano instantâneo em um
ponto de coordenadas ![]() devido a um evento
ocorrido no ponto
devido a um evento
ocorrido no ponto ![]() no mesmo instante
de tempo. Observe-se
que o potencial escalar nesse caso
não exibe o retardo entre causa e efeito que se conhece
devido à velocidade
finita de propagação de perturbações eletromagnéticas. Ou
seja, nesse gauge,
rigorosamente o potencial escalar não tem significado
físico. No entanto, em
situações em que os tempos de retardo entre causa e efeito
podem ser
desprezados, i.e., quando as distâncias envolvidas são
muito pequenas
relativamente ao comprimento de onda típico da perturbação
eletromagnética, o
potencial escalar obtido no gauge de Coulomb descreve um
campo quase-estático,
com interpretações físicas semelhantes àquelas descritas
na eletrostática.
no mesmo instante
de tempo. Observe-se
que o potencial escalar nesse caso
não exibe o retardo entre causa e efeito que se conhece
devido à velocidade
finita de propagação de perturbações eletromagnéticas. Ou
seja, nesse gauge,
rigorosamente o potencial escalar não tem significado
físico. No entanto, em
situações em que os tempos de retardo entre causa e efeito
podem ser
desprezados, i.e., quando as distâncias envolvidas são
muito pequenas
relativamente ao comprimento de onda típico da perturbação
eletromagnética, o
potencial escalar obtido no gauge de Coulomb descreve um
campo quase-estático,
com interpretações físicas semelhantes àquelas descritas
na eletrostática.
Para o potencial vetor
obtém-se
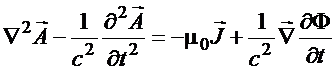
Da solução para o
potencial tem-se
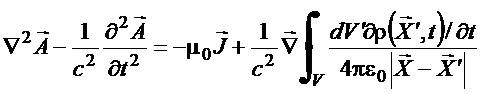
Copyrigth 1999-2013 by Eduardo Fontana
Do princípio da
conservação da carga

e portanto
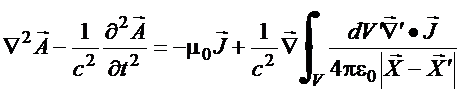 (29)
(29)
Para obter uma equação
diferencial mais simples
para o potencial vetor, seja a decomposição do vetor
densidade de corrente em
duas componentes
![]() (30)
(30)
com
![]() componente
longitudinal
(irrotacional)
componente
longitudinal
(irrotacional)
![]() componente
transversal
ou solenoidal (sem divergência)
componente
transversal
ou solenoidal (sem divergência)
Isso pode sempre ser
realizado, uma vez que pelo
teorema de Helmholtz um vetor é completamente especificado
pelo seu divergente
e rotacional e sua componente normal no domínio de
existência do vetor.
Essa decomposição significa apenas que as
componentes acima definidas contém essas informações
básicas acerca do vetor
densidade de corrente.
Copyrigth 1999-2013 by Eduardo Fontana
Para vermos isso, notemos
que
![]() ,
,
ou seja
 (31)
(31)
Da mesma forma tem-se
![]() ,
,
ou seja
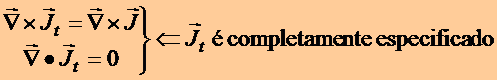 (32)
(32)
A especificação é completa
se forem conhecidas
as components normais de ambos os vetores. Se a
distribuição é localizada e o
domínio é uma esfera imaginária de raio infinito, o vetor
J e suas componentes
são nulas na superfície.
Obtenção
das componentes longitudinal e transversal
De (31) pode-se escrever
![]() (33)
(33)
Copyrigth 1999-2013 by Eduardo Fontana
Ou seja, a função ![]() satisfaz
à eq de
Poisson e tem como solução
satisfaz
à eq de
Poisson e tem como solução
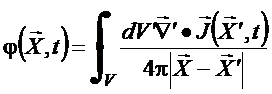 (34)
(34)
e portanto
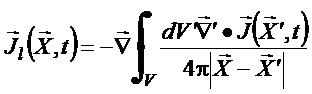 (35)
(35)
De (31) pode-se escrever
![]() (36)
(36)
Escolhendo ![]() tal que
tal que ![]() , obtém
, obtém
![]()
cuja solução é
 (37)
(37)
Portanto
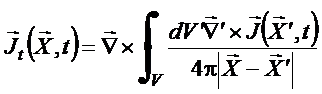 (38)
(38)
Copyrigth 1999-2013 by Eduardo Fontana
Da Eq.(29) tem-se
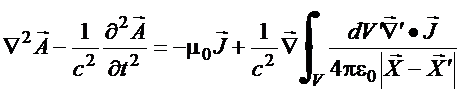
ou ainda

e da Eq.(17)

o que fornece
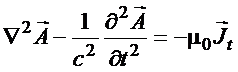 (39)
(39)
que só depende da
componente transversal, dada
pela Eq.(37).
Portanto no gauge de
Coulomb, o potencial
escalar magnético é dado pelo potencial coulombiano
instantâneo dado pela
Eq.(34) e o potencial vetor satisfaz à eq. da onda
não-homogênea (38) que só
depende da componente transversal do vetor densidade de
corrente.
Copyrigth 1999-2013 by Eduardo Fontana
25.4 Função de Green para a equação de Helmholtz
A forma geral da equação
da onda para quaisquer
grandezas envolvidas reduz-se a uma equação escalar do
tipo
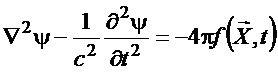 (40)
(40)
O termo ![]() representa a fonte
da equação. A solução geral
e sua natureza podem ser inferidas determinando-se a
função de Green
correspondente.
representa a fonte
da equação. A solução geral
e sua natureza podem ser inferidas determinando-se a
função de Green
correspondente.
Assume a ausência de
superfícies de fronteira,
por simplicidade. Usa
a transformada
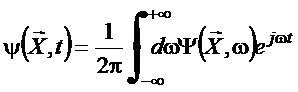 (41)
(41)
 (42)
(42)
Para obter a transformada
inverse usa
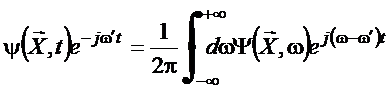 ,
,
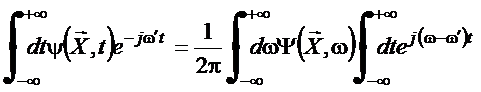 ,
,
Copyrigth 1999-2013 by Eduardo Fontana
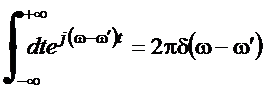 ,
,
donde

ou equivalentemente
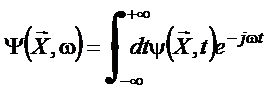 ,
(43)
,
(43)
 .
(44)
.
(44)
Inserindo as expressões
(41) e (42) na eq. da
onda obtém

Como as expansões em ambos
os membros são
únicas, os coeficientes da expansão em ambos os membros
são iguais, i.e.,
![]() (45)
(45)
com
 (46)
(46)
Copyrigth 1999-2013 by Eduardo Fontana
sendo definido como o
“número de onda”. A
Eq.(45) é a equação de Helmholtz. A função de
Green para a eq. de Helmholtz é
obtida de
![]() (47)
(47)
Na ausência de superficies
de fronteira, ou
equivalentemente, no espaço ilimitado, o efeito em ![]() produzido
por
uma perturbação ou impulso em
produzido
por
uma perturbação ou impulso em ![]() só
depende da
distância
só
depende da
distância ![]() , e
portanto a
função de Green depende da distância, i.e.,
, e
portanto a
função de Green depende da distância, i.e.,
![]() (48)
(48)
De (47)
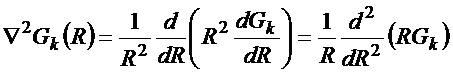
ou equivalentemente
 (49)
(49)
com
![]() ,
(50)
,
(50)
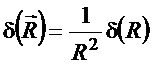 (52)
(52)
Copyrigth 1999-2013 by Eduardo Fontana
Para ![]() tem-se a equação
homogênea
tem-se a equação
homogênea
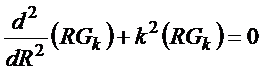
cuja solução é da forma
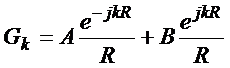 (53)
(53)
![]() (49) reduz-se a
(49) reduz-se a
![]()
cuja solução é bem
conhecida, ou seja
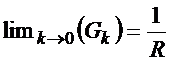
e de (53) essa condição
leva a
![]() (54)
(54)
Assim
![]() (55)
(55)
com
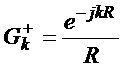 (56)
(56)
Copyrigth 1999-2013 by Eduardo Fontana
 (57)
(57)
As soluções (56) e (57)
são ambas constantes em
qualquer superfície esférica e são ondas eféricas. Como é bem
sabido (56) representa uma onda
esférica divergente a partir da origem, que é o ponto no
espaço onde se dá o
impulso no segundo membro da equação de Helmholtz para a
função de Green. A
expresão (57) representa uma onda esférica
convergente para a origem. Se uma fonte
física estivesse presente na
origem, essa segunda solução não seria uma solução física
do problema, pois
violaria o princípio de causa e efeito. É apenas uma
solução do problema
matemático. No entanto soluções convergentes podem existir
fisicamenteem outras
situações em que a fonte não esteja localizada na origem.
25.5 Função de Green para a equação da onda
Consideremos agora a
determinação da função de
Green para a equação da onda, i.e.,
 (58)
(58)
Usando
 (59)
(59)
Copyrigth 1999-2013 by Eduardo Fontana
e a transformada de
Fourier da função temporal
 (60)
(60)
e após igualar os
coeficientes das expansões em
ambos os membros de (58), obtém a eq. de Helmholtz (47),
i.e.,
![]()
cuja solução é dada por
(55). Associada
a cada componente da solução tem-se
a solução temporal correspondente
 (61)
(61)
com
![]() (62)
(62)
Utilizando (56) e (57),
 (63)
(63)
Dessa expressão tem-se
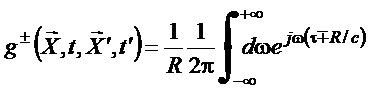
Copyrigth 1999-2013 by Eduardo Fontana
e a integração fornece
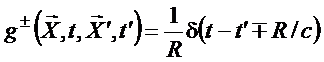
que, devido à função delta
ser par, pode ser
posta na forma
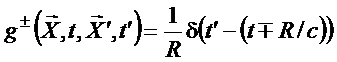 (64)
(64)
As soluções individuais são
 (65)
(65)
Pelo teorema de Green, a
solução geral da
equação da onda é portanto
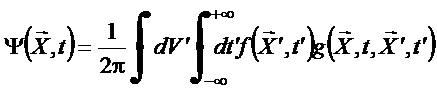
A solução física é aquela
que contém o
princípio de causa-efeito, e tem de conter apenas a função
de Green retardada ![]() , ou seja
, ou seja
 (66)
(66)
Copyrigth 1999-2013 by Eduardo Fontana
Utilizando (65) obtém
 (67)
(67)
Essa expressão mostra a
relação causa-efeito. Ou
seja, o efeito no tempo t é produzido
por perturbação no tempo anterior ![]() . Uma fonte pontual
localizada produz
perturbação esférica divergente. A solução geral é uma
combinação dessas
contribuições. Cada onda esférica divergente se propaga
com a velocidade da luz
c.
. Uma fonte pontual
localizada produz
perturbação esférica divergente. A solução geral é uma
combinação dessas
contribuições. Cada onda esférica divergente se propaga
com a velocidade da luz
c.
