PGEE936 - Eletromagnetismo Avançado - PPGEE

PGEE936 - ELETROMAGNETISMO AVANÇADO

INFORMES

Programa da Disciplina
1. Revisão de Álgebra Vetorial
2. Eletrostática no vácuo e em meios dielétricos
3. Problemas de Valores de Fronteira em Eletrostática
4. Condução Elétrica
6. Magnetostática
7. Lei de Faraday, Corrente de Deslocamento e Equações de Maxwell para Campos Dinâmicos.
8. Ondas eletromagnéticas, atenuação e dispersão.

CRONOGRAMA 2023.01

LOCAIS E HORÁRIOS
4as.: 13h - 15h - Telemática, DES-CTG-UFPE
6as.: 13h-15h - Telemática, DES-CTG-UFPE

DATAS DOS EXAMES

EXAME	1	2	3	4	5	6
DATA	05/04/2023	26/04/2023	12/05/2023	31/05/2023	16/06/2023	05/07/2023

NOTAS DE AULA

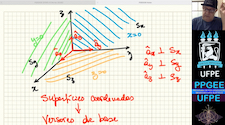
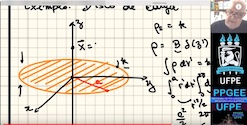
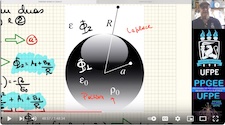
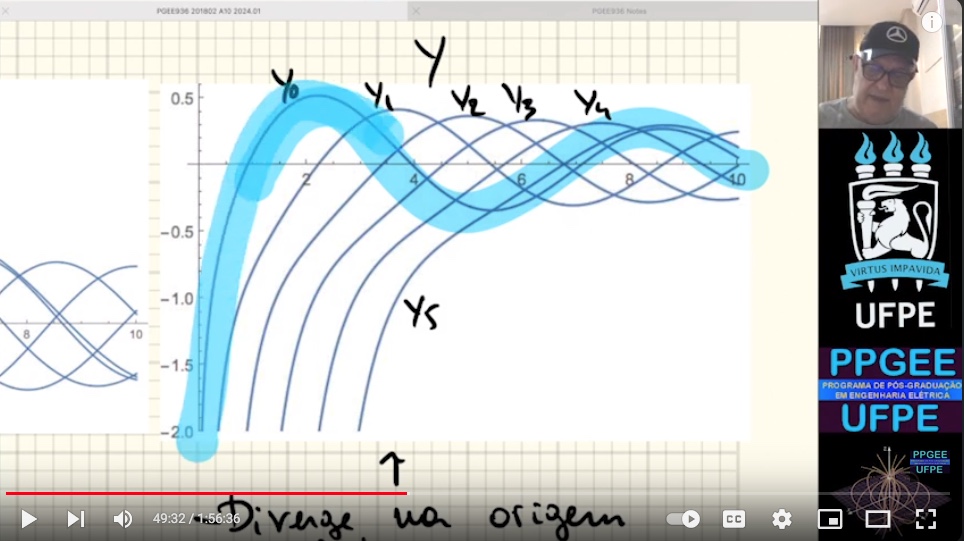
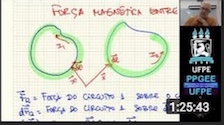
A1. Introdução, álgebra vetorial, alguns sistemas de coordenadas, transformações entre sistemas de coordenadas
A2. Integração no espaço 3D, diferenciação no espaço 3D, gradiente, divergente.
A3. Divergente, rotacional, identidades de Green, teoremas de Gauss, Stokes e Helmholtz
A4. Elementos de Eletrostática. Campo de sistemas discretos e distribuições contínuas. Função densidade para uma carga discreta. Funções delta no espaço 3D. Lei de Gauss, Potencial elétrico.
A5. Exemplos de cálculos de potencial de distribuições representadas por funções delta. Energia potencial. Eqs. de Maxwell para eletrostática no vácuo. Condições de contorno.
A6. Dipolo elétrico. Polarização, cargas de polarização. Determinação de campos em meios materiais com o emprego do conceito de cargas de polarização. Relação constitutiva em meios dielétricos. Forma final das eqs. de Maxwell para eletrostática. Tipos de dielétricos.
A7 Energia em meios dielétricos. Eqs. de Poisson e Laplace. Exemplos de solução da eq. de Poisson para problemas de alta simetria. Solução integral para a função potencial. Solução com o emprego de funções de Green. Teorema da unicidade.
A8. Solução da Eq. de Laplace por separação de variáveis. Separação de variáveis em coordenadas cartesianas. Expansões em funções ortogonais. Solução da Eq. de Laplace para problemas bidimensionais em cilíndricas. Solução numérica da eq. de Laplace.
A9. Separação de variáveis em esféricas, polinômios de Legendre, polinômios associados de Legendre, Harmônicos. Teorema da Adição para Harmônicos Esféricos.
A10. Separação de variáveis em coordenadas cilíndricas. Funções de Bessel. Ortogonalidade das Funções de Bessel. Funções Modificadas de Bessel. Transformada de Fourier-Bessel. Expansão da função inversa em cilíndricas.
A11. Método das imagens para interface planar. Função de Green para interface planar.
A12. Método das imagens para fronteiras esféricas ou cilíndricas. Funções de Green para superfícies esféricas.
A13. PVF e Método das Imagens em Meios Dielétricos.
A14. Corrente elétrica. Densidade de corrente. Lei de Ohm. Princípio da conservação da carga. Intercâmbio de energia entre campo e portadores de carga. PVF em meios condutores.
A15. Força magnetostática, densidade de fluxo magnético. Potencial vetor magnético. Eqs. de Maxwell para a Magnetostática no vácuo.
A16. Determinação de campos com a formulação integral. Potencial vetor e campo da espira de corrente. Campo de distribuição localizada. Dipolo magnético, Magnetização. Corrente de magnetização. Vetor campo magnético. Equações de Maxwell para a Magnetostática. Tipos de meios materiais do ponto de vista magnético, permeabilidade magnética.
A17. Uso dos potenciais vetor e escalar na solução de PVF em meios magnéticos.
A18. Lei de Faraday. Indutância e energia magnética. Corrente de desolocamento.
A19. Eqs. De Maxwell para campos variantes no tempo, teorema de Poynting.
A20. Equação da onda homogênea. Solução geral de eq. da onda. Eqs. De Maxwell no regime harmônico.
A21. Equação da onda não-homogênea. Gauge de Lorentz e de Coulomb. Solução geral de eq. da onda não homogênea.
A22. Teorema de Poynting no regime harmônico. Onda plana no regime harmônico.
A23. Resposta em frequência de meios materiais. Atenuação.
A24. Resposta em frequência de meios materiais. Dispersão.

VIDEOAULAS

VA1 - 22/03/2023	VA2 - 24/03/2023	VA3 - 29/03/2023	VA4 - 31/03/2023
VA5 - 05/04/2023	VA6 - 12/04/2023	VA7 - 14/04/2023	VA8 - 19/04/2023
VA9 - 21/04/2023	VA10 - 28/04/2023	VA11- 03/05/2023	VA12 - 05/05/2023
VA13 -10/05/2023	VA14 - 17/05/2023	VA15 - 19/05/2023	VA16 - 24/05/2023
VA17-26/05/2023	VA18 - 02/06/2023	VA19 - 07/06/2023	VA20 - 09/06/2023
VA21 - 14/06/2023	VA22 - 21/06/2023	VA23 - 23/06/2023	VA24 - 28/06/2023

LISTAS DE EXERCÍCIOS 2023.01

Lista 01 | Lista 02 | Lista 03 | Lista 04 | Lista 05 | Lista 06 |
|Problemas do Jackson 3a. ed. |Cap.1 | Cap.2 | Cap.3 | Cap.4| Cap.5 |

REFERÊNCIAS BÁSICAS

Eduardo Fontana, "Tratado de Eletromagnetismo", Editora da Unicamp, 1a. Edição, Versão E-Pub (2022) (Amazon | Apple Books)
Eduardo Fontana, "Tratado de Eletromagnetismo", Editora da Unicamp, 1a. Edição, Versão impressa (2021)
J. D. Jackson, "Classical Electrodynamics," 3rd. edition, Wiley 1998

REFERÊNCIAS SUPLEMENTARES

G. B. Arfken, " Mathematical Methods for Physicists," 6th edition, Elsevier (2005).

James Clerk Maxwell, "A Treatise on Electricity and Magnetism," Vol. 1, Oxford (1873) - on line

Simon Ramo, John R. Whinnery and Thodore Van Duzer, " Fields and Waves in Communication Electronics", 3rd edition (1994).

Eduardo Fontana, "Tutorial Mathcad Parte I"

Eduardo Fontana, "Tutorial Mathcad Parte II"

LINKS ÚTEIS

Eduardo Fontana - Portal de Conteúdo

Programa de Pós-Graduação em Engenharia Elétrica da UFPE

Canal Youtube da Pós-Graduação em Engenharia Elétrica da UFPE

Departamento de Eletrônica e Sistemas da UFPE

Wikipedia - Enciclopédia web

Mathworld - Base de Referência em Matemática

Portal de Periódicos CAPES

No ar desde 12/08/2017

Visitante

Desde 19/08/2017

Última atualização: 23/05/2023